Theoretical energy savings

We next present a theoretical analysis of the energy savings obtained when DPM/DVS is combined with user delay modeling.

For simplicity of exposition, consider two performance levels of the system from a pool of performance levels for a given user delay. Let $D$ denote the user delay, $P$ the system power consumption for the higher performance level, and $P'$ that for the lower one. The energy consumption for the system during the user delay without DPM/DVS will be

$$E = D{\cdot}P\vspace*{-2.2mm}$$

Suppose we can predict the user delay perfectly, change the system performance to the lower one after the system finishes responding, and change it back to the higher one right before the next user input. Let $P_{HL}$ and $P_{LH}$ denote the performance level transition power, and $T_{HL}$ and $T_{LH}$ denote the delay for higher-to-lower and lower-to-higher transitions, respectively. We also assume that $D>(T_{HL}+T_{LH})$. Then the energy consumption for the system during the user delay with such a performance-level transition is given by

$$\begin{eqnarray*} E_0 = (D-T_{HL}-T_{LH}){\cdot}P' +\\ \vspace*{-6mm} T_{HL}{\cdot}P_{HL} + T_{LH}{\cdot}P_{LH}\vspace*{-6mm} \end{eqnarray*}$$

The energy saving is therefore

$$\begin{eqnarray*} \lefteqn{{\Delta}E_0=E-E_0=D\cdot(P-P')}\vspace*{-6mm}\\ &&-T_{HL}(P_{HL}-P')-T_{LH}(P_{LH}-P') \vspace*{-1mm} \end{eqnarray*}$$

If we assume $P=P_{HL}=P_{LH}$, we have

$$\begin{eqnarray*}{\vspace*{-1mm}\Delta}E_0 =\{D-(T_{HL}+T_{LH})\}\cdot(P-P') \end{eqnarray*}$$

The energy saving ratio is calculated as

$$\begin{eqnarray*} {\rho}_0=\frac{{\Delta}E_0}{E} =\{1-\frac{(T_{HL}+T_{LH})}{D}\}\cdot(\frac{P-P'}{P}) \end{eqnarray*}$$

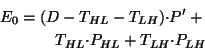
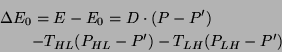
If the system changes the performance level upon a user input, we can obtain the energy saving through a similar analysis as

$$\begin{eqnarray*} {\rho}'=\rho_0-\frac{T_{LH}}{D}\cdot\frac{P'}{P}\vspace*{-4mm} \end{eqnarray*}$$

If the delay models are used to predict $D$ as $D'$ and the system is put into the low performance level if $D'>(T_{HL}+T_{LH})$ and put back into the high performance level right before the predicted user delay elapses, we have

$${\rho}=\left\{%% \begin{array}{ll} \rho_0-\frac{T_{LH}}{D}\c... ...{+1.5mm}\\ 0,&D'{\leq}(T_{HL}+T_{LH}). \end{array}%% \right.$$

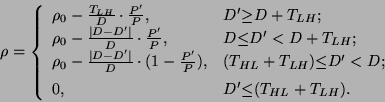
Given the two performance levels, the energy saving ratio is only dependent on the user delay and prediction error. Comparing $\rho$ with $\rho'$, we can see that using predicted user delay is actually more energy-efficient if $T_{LH}$ is large compared with user delay prediction errors. Note that both $\rho$ and $\rho'$ can be negative, which means energy consumption can be actually increased if performance-level transition is not properly done.