

Next: Utilizing User Delays for
Up: Dynamic Power Optimization of
Previous: Motor delay
History-based User Delay Model
The psychological model is content-based. It
predicts user delay length knowing what users will see. In some
cases, it may be difficult to know beforehand the user interface
content. Therefore, we devise a user delay model based on history,
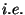 , multiple observations from the past. It works in a fashion
similar to the median filter in order to filter out randomness in
user behavior. Let
, multiple observations from the past. It works in a fashion
similar to the median filter in order to filter out randomness in
user behavior. Let 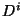 denote the
denote the 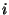 th last observed delay for
an STD state and
th last observed delay for
an STD state and 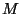 the total number of user delays recorded for
that state.
the total number of user delays recorded for
that state.
The delay record is sorted to generate a new series so that
Then we define the habitual set 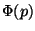 as
as
where
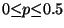 with a typical value of
with a typical value of
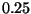 .
. 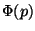 contains the central
contains the central
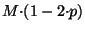 items of the sorted series. It is a set extension of the concept
of a median. Let
items of the sorted series. It is a set extension of the concept
of a median. Let 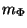 denote the mean of
denote the mean of 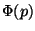 . Then the
next user delay for the state is predicted as
. Then the
next user delay for the state is predicted as
where 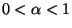 .
. 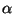 is called the
is called the 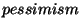 factor.
factor.
When 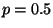 , the above approach reduces to using the median of
the delays in the recorded history. When
, the above approach reduces to using the median of
the delays in the recorded history. When 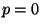 , it reduces to
using the mean instead.
, it reduces to
using the mean instead.


Next: Utilizing User Delays for
Up: Dynamic Power Optimization of
Previous: Motor delay
Lin Zhong
2003-12-20
![]() , the above approach reduces to using the median of
the delays in the recorded history. When
, the above approach reduces to using the median of
the delays in the recorded history. When ![]() , it reduces to
using the mean instead.
, it reduces to
using the mean instead.